- 1a)
- Geben Sie eine 4x4 Matrix
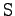 an, welche bei
Multiplikation von links her
an, welche bei
Multiplikation von links her
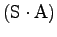 alle Zeilen um einen Platz nach unten verschiebt, und
zuoberst eine Zeile mit lauter Nullen erzeugt!
alle Zeilen um einen Platz nach unten verschiebt, und
zuoberst eine Zeile mit lauter Nullen erzeugt!
- L1a)
-

- 1b)
- Wie kann man nachweisen, dass die Matrix der reinen
Spiegelung an der y-Achse
(ohne Translation!)
in 2D homogenen Koordinaten eine orthogonale Matrix ist?
- L1b)
- Das Produkt M'*M ergibt die Einheitsmatrix I. Alle Diagonalelemente
sind 1 oder minus 1, beides gibt quadriert plus 1.
- 1c)
- Geben Sie die Buchstabengruppe an, mit der ein MATLAB-plot-Befehl
sowohl eine durchgezogene schwarze Linie als auch schwarze stehende
Kreuze als Marker
zeichnet!
- L1c
- plot(x,y,'k-+')
- 1d)
- Wieso ist die Methode zur Lösung von linearen Gleichungssystemnen
nach der Kramerschen Regel für grosse Gleichungssysteme
nicht zu empfehlen?
- L1d
- Weil der Rechenaufwand im Vergleich zu den gebräuchlichen
Algorithmen, wie z.B. Gauss-Elimination, viel zu stark ansteigt mit
steigender Anzahl der Unbekannten.
Geben Sie die MATLAB-Befehle an, um zwei ganze Umgänge der Kurve in schwarzer Farbe zu zeichnen und zusätzlich die vorgeschriebenen Punkte durch rote Ringe zu markkieren
% fuer w = 0 ist r = 0.2 r0 = 0.2 % fuer w = pi ist r = 3.2 % a*w*w ist also 3 a = 3/pi^2 w = (0:0.01:2)*2*pi r = r0+ a*w.^2 polar(w,r,'k') hold on plot([0.2 -3.2] , [0 0], 'ro') hold off
ABCD und EFGH sind horizontal, also ist der Normalenvektor in z-Richtung: Deren Distanzen zum Ursprung (Hoehenpositionen) sind 0 und 2 ABCD : [ 0 0 1]' * OP = 0 ; EFGH : [ 0 0 1] * OP - 2= 0; ABFE und DCGH sind vertikal , parallel zur xz Ebene, der Normalenvektor ist in y-Richtung: Deren Distanzen zum Ursprung sind 0 und 2 ABFE : [ 0 1 0]' * OP = 0 ; DGCH : [ 0 1 0] * OP - 2 = 0; AEHD und BCGF sind vertikal , parallel zur yz Ebene der Normalenvektor ist in x-Richtung: Deren Distanzen zum Ursprung sind -1 und 1 AEHD : [ 1 0 0]' * OP + 1 = 0 ; BGCF : [ 1 0 0] * OP - 1 = 0; % zur Verifikation: immer die Punkte die zur Ebene gehoeren geben Null % und selektieren dann den Buchstaben mit logischen Index-Array W = [ -1 1 1 -1 -1 1 1 -1; 0 0 2 2 0 0 2 2; 0 0 0 0 2 2 2 2] ; S = 'ABCDEFGH'; ebd = [0 0 1] * W ; S(ebd==0) , ebd = [0 0 1] * W - 2; S(ebd==0) ebd = [0 1 0] * W ; S(ebd==0) , ebd = [0 1 0] * W - 2; S(ebd==0) ebd = [ 1 0 0] * W + 1 ; S(ebd==0) , ebd = [1 0 0] * W - 1 ; S(ebd==0)
Dor = [ 0 -4 -4 0; -8 -8 -4 -8; 1 1 1 1] Sz = [ 1 0 -2; 0 1 0; 0 0 1], Sb = [ 1 0 2; 0 1 0; 0 0 1], Myax = [ -1 0 0; 0 1 0; 0 0 1], Mxax = [ 1 0 0; 0 -1 0; 0 0 1], Tt = Mxax*Sb*Myax*Sz % = [ -1 0 4; 0 -1 0; 0 0 1] Dt = Tt * Dor % = [ 4 8 8 4; 8 8 4 8; 1 1 1 1]
xf = linspace(-pi/4, pi/4, 7) yf = cos(xf) A = [xf.^2; xf; ones(1,7)]' ; p = A\yf' xc = -pi/4:0.01:pi/4 yc = p(1)*xc.^2 + p(2)*xc + p(3) plot(xc,yc) ; hold on plot(xf,yf,'ro'); hold off
unter der Nebenbedingung
syms x y z w L = (x^2 + y^2+ z^4)^(1/4) + w*(-z-y+x^2 +10 ) diff(L,x) % 1/2/(x^2+y^2+z^4)^(3/4)*x+2*w*x diff(L,y) % 1/2/(x^2+y^2+z^4)^(3/4)*y-w diff(L,z) % 1/(x^2+y^2+z^4)^(3/4)*z^3-w diff(L,w) % -z-y+x^2+10
