HS08 - Lösungen zur Prüfung 1, R-G-B-Y, 18.November2008

R   Ingenieurmathematik Prüfung 1 18.November2008
Zeit 90 Minuten, Reihenfolge beliebig, 8 Punkte pro Hauptaufgabe, 40 Pt. = N.6.

1)

Verständnisfragen: Es werden nur ganz kurze Antworten erwartet.

1a)

Wie lautet (ungefähr! sinngemäss, nicht genauer Wortlaut) die Fehlermeldung, wenn man zwei Zeilenvektoren eigentlich Elementweise multiplizieren wollte, aber irrtümlich den mormalen statt den Punkt-Operator eingesetzt hat?

L 1a)

``inner dimensions must agree''

1b)

Wie erreicht man, dass in MATLAB die nachfolgenden plot-Aufrufe in dasselbe Zeichenfeld eingefügt werden?

L 1b)

hold on

1c)

Wieviele Nullen muss eine Rechts-Dreiecksmatrix der Dimension nxn mindestens enthalten?

L 1c)

$n^2/2 -n/2 = n*(n-1)/2$

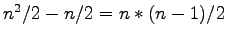
1d)

Für welche Werte von n gibt es mindestens eine relle Lösung der Gleichung $z^n+1=0$ ?

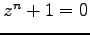L 1d)

für ungerade Werte von n.

L 2)

Schreiben Sie ein MATLAB-Skript, welches alle Lösungen der komplexen Gleichung

$$z^4 + 4~j = 0$$

als rote Kreise einzeichnet, und dazu in der gleichen Figur in schwarzer Farbe den Kreis zeichnet, auf dem diese Lösungen alle liegen.

L 2)

zs = 4^(1/4)*[ exp(j*(3*pi/8)) exp(j*(7*pi/8)) exp(j*(11*pi/8)) exp(j*(15*pi/8))]
t = (0:0.01:1)*2*pi;
plot(zs,'ro') ; hold on; plot( 4^(1/4)*exp(j*t), 'k'); hold off;
axis equal

3)

Das rechtwinklig gleichschenklige Dreieck A=[2 4]', B=[-2 4]', C=[0 2]' soll um den Mittelpunkt seiner Hypotenuse um den Winkel 180 Grad gedreht werden. Geben Sie die Matrizen der Teiltransformationen in homogenen Koordinaten der Ebene an und die Gesamt-Transformationsmatrix, sowie die Eck-Koordinaten des Bildes.

L 3)

A = [2; 4; 1]; B = [-2; 4; 1]; C = [0; 2; 1];
lin = [ A B C A];
M = A+B/2;  % = [0 ; 4] 
Tz = [ 1 0 0; 0 1 -4; 0 0 1]
R =  [ -1 0 0; -0 -1 0; 0 0 1]
Tb = [ 1 0 0; 0 1 4; 0 0 1]
Tt = Tb*R*Tz    % = R =  [ -1 0 0; 0 -1 8; 0 0 1]
lint = Tt*lin   
plot(lin(1,:), lin(2,:)); hold on ;
plot(lint(1,:), lint(2,:),'r'); axis equal; hold off

4)

Im regulären Oktaeder ABCDSK ( A=[ 0; -8; 0], B=[ 8; 0; 0], C=[ 0; 8; 0], D=[-8; 0; 0], S=[0; 0; 8], K=[0; 0; -8] , ABCD in Mittelebene, S = Spitze,K = Keller) wird eine Ebene durch die 4 Punkte A,D, MB und MC gelegt, wobei MB der Mittelpunkt der Strecke BS ist und MC der Mittelpunkt der Strecke CS. Bestimmen Sie die Hesse'sche Normalform dieser Ebene und berechnen Sie die Abstände der beiden Punkte S und Z=(0/0/0) von dieser Ebene.

L 4)

A=[ 0; -8; 0]; B=[ 8; 0; 0]; 
C=[ 0;  8; 0]; D=[-8; 0; 0]; 
S=[ 0;  0; 8]; K=[ 0; 0; -8];
lin = [A S C K A B S D K B C D A];
plot3(lin(1,:), lin(2,:), lin(3,:)); axis equal
hold on
MB = (B+S)/2; MC = (C+S)/2; leb = [D A MB MC D];
plot3(leb(1,:), leb(2,:), leb(3,:),'r');
hold off
v = D-A ; w = MB-A; 
N = cross(w,v) ; en = N/norm(N)
dk = en'*A       %  Abstand 0/0/0 = -dk
dkt = en'*MC -dk %  = Test ob 4. Punkt auf gleicher Ebene
ds = en'*S -dk

5)

Bestimmen Sie die Parameterdarstellung der linksgängigen Schraubenlinie einer Drosselspule mit Radius 15 cm, Ganghöhe 1.5 cm und Gesamthöhe 30 cm. Die Achse verläuft entlang der z-Achse, der Startpunkt ist bei (15/0/0) und der Endpunkt bei (15/0/30). Geben Sie die MATLAB-Befehle an für das Zeichnen dieser Schraubenlinie.

L 5)

R = 15 ; h = 1.5; Zmax = 30;
nturn = Zmax/h
t = (0:0.01:nturn)*2*pi;
x = R*cos(t) ; y = -R*sin(t); z = t*h/(2*pi);
plot3(x,y,z) ; axis equal; hold on
plot3(15, 0, 0,'ro'); plot3(15, 0, 30,'ro'); hold off

6)

Geben Sie die Formeln an für die ersten drei unbekannten Werte, die beim Vorwärts-Einsetzen in einer bekannten Matrix L der Dimension 9x9 aus der L-R-Zerlegung und einem neuen Vektor der rechten Seiten b ausgewertet werden. (Das Vorwärts-Einsetzen dient der Bestimmung von y in L*y = b.

L 6)

$y_1 = b_1$
$y_2 = b_2 - L_{21} \cdot y_1$
$y_3 = b_3 - L_{31} \cdot y_1 - L_{32} \cdot y_2$