HS 09/10 - Lösung zur Prüfung 1, B, 17. Nov. 2009

B   Ingenieurmathematik Prüfung 1 17.Nov.2009
Zeit 90 Minuten, Reihenfolge beliebig, 8 Punkte pro Hauptaufgabe, 40 Pt. = N.6.

1)

Verständnisfragen: Es werden nur ganz kurze Antworten erwartet.

1a)

Wieviele Nullen hat eine Diagonalmatrix der Dimension nxn mindestens?

1b)

Wie lautet die Gleichung, mit der das erste Element beim Rückwärts-Einsetzen in einer 5x5 Matrix bestimmt wird? (d.h. Ergänzen Sie $x_? = ???$)

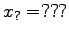1c)

Bestimmen Sie die die Inverse der Matrix 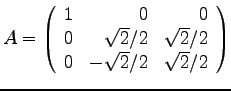$${ A = \left( \begin{array}{rrr} 1 & 0 & 0 \\ 0 & \sqrt{2}/2 & \sqrt{2}/2 \\ 0 & -\sqrt{2}/2 & \sqrt{2}/2 \\ \end{array} \right) }$$ mit Hilfe der Angabe dass die Matrix A orthogonal ist.

1d)

Mit welchen MATLAB Befehlen erreicht man, dass die Grafik in einem quadratischen Feld gezeichnet wird und dabei die x-Werte zwischen -4 und 4 und die y-Werte zwischen 0 und 8 variieren?

2)

Suchen Sie die speziellen Permutations/Auswahlmatrizen $Pl$ und $Pr$, so dass die folgende Matrizengleichung für beliebige Werte der Matrix A gilt!
$${ \left( \begin{array}{rrrrr} 0 & 0 & 0& 0 & 0 \\ 0 & 0 & 0... ..._2 & e_3 & e_4 & e_5 \end{array} \right) \cdot Pr ~=~ Pl \cdot A \cdot Pr }$$

3)

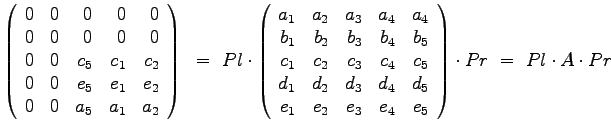
Geben Sie die MATLAB-Befehle an, mit denen ein Vektor v aus komplexen Zahlen erzeugt wird, welcher beim Aufruf plot(v); axis equal ein reguläres Achteck zeichnet, das im Kreis um $(0/0)$ mit dem Radius 5 einbeschrieben ist. Geben Sie auch die MATLAB-Befehle an zum Zeichnen des zugehörigen Umkreises.

L3)

 k = 0:8; w = 2*pi/8*k
 z8 = 5*exp(i*w)
plot(z8)
hold on
axis equal
t = (0:0.005:1)*2*pi;
kr = 5*exp(i*t);
plot(kr,'k')
hold off

4)

Gegeben ist ein Keil mit der Grundfläche ABCD und der Oberkante EF durch $A(0/0/0)$, $B(0/-12/0)$ , $C(5/-12/0)$, $D(5/0/0)$ und $E(0/0/5)$, $F(5/0/5)$ .
Bestimmen Sie je die Ebenengleichung der Deckfläche und der Grundfläche in der Hesse'schen Normalform, sowie die Neigung der Deckfläche!

L5)

A  = [0 0 0]'; B = [0 -12 0]'; C = [5 -12 0]';
D = [5 0 0]' ; E = [0 0 5]' ; F = [5 0 5]';
Kl = [A B C D A E B E F C F D];
plot3(Kl(1,:),Kl(2,:),Kl(3,:),'m')
axis equal
eng = [ 0 0 1]', dkritg = 0
%   Tests ob A,B,C,D in Grundflaeche
dtA = eng'*A-dkritg, dtB = eng'*B-dkritg, 
dtC = eng'*C-dkritg, dtD = eng'*D-dkritg, 
%   2 Vektoren in Deckflaeche BCFE
u = B-E, v = C-E
N = cross(u,v)             % = [ 0 -25 60]
nN = norm(N)               %  = 65
endf = N/nN                % = [0 -0.3846  0.9231]
dkritdf = endf'*E          %  = 4.6154
%   Tests ob B,C,F auch in Grundflaeche
dtdB = endf'*B-dkritdf, dtdC = endf'*C-dkritdf, 
dtdF = endf'*F-dkritdf
%   Winkel direkt acos S-prod zwischen Einheitsvektoren
wneig = acos(endf'*eng)    % 0.3948 rad
wneigd = wneig*180/pi      % = 22.6154 Grad

5)

Suchen Sie die Teil-Transformationsmatrizen und die Gesamt-Transformations-Matrix, in homogenen Koordinaten der Ebene, welche das Quadrat ABCD mit den Ecken $A =(0/0)$, $B=(-6/6)$, $C=(-12/0)$, $D=({-6} / {-6})$ um $-90^{\mathrm{o}}$  (im Uhrzeigersinn) um seinen Mittelpunkt dreht. Bestimmen Sie auch die gedrehten Koordinaten ÃBCD.
Geben Sie auch ein MATLAB-Skript an, das diese Transformation in homogenen Koordinaten durchführt und das Urbild und Bild in eine gemeinsame Grafik einzeichnet.

L5)

Qo = [0 -6 -12 -6 0; 0 6 0 -6 0; 1 1 1 1 1];
%  Mittelpunkt quadrat ist A+B+C+D/4  =[ -6 0]'
Tz = [ 1  0  6; 0 1 0; 0 0 1]
R = [0 1 0 ; -1 0 0; 0 0 1]
Tb = [ 1  0 -6; 0 1 0; 0 0 1]
Ttot = Tb*R*Tz
Qt = Ttot*Qo
plot(Qo(1,:),Qo(2,:),'g') 
hold on 
plot(Qt(1,:),Qt(2,:),'ro')
axis equal ;  hold off

6)

Suchen Sie die Darstellungen der beiden Schraubenlinien-Stücke mit Achse auf der z-Achse, welche beide im Punkt $(5/0/0)$ starten, und im Punkt $(-5/0/2)$ enden und dazwischen je eine halbe Umdrechung ausführen. Eines der Schraubenlinien-Stücke soll linksdrehend, das andere rechtsdrehend sein.
Schreiben Sie ein MATLAB-Skript zur simultanen Darstellung der beiden Kurvenstücke!

L6)

t = (0:0.05:1)*pi  % eine halbe Drehung
%  Vorschub ist 2 pro halbe Drehung, also ist g = 4
g = 4
z = t*g/(2*pi);  % gleiches z fuer beide
%  Winkel 0 ist bei 5 0, also R = 5
R = 5
%  Vorschub nach oben, also Gegenuhrzeiger in x-y Ebene ist rechtsdrehend
xr = R*cos(t); yr = R*sin(t);
%  Uhrzeigersinn in x-y Ebene ist linksdrehend
xl =  R*cos(t); yl = -R*sin(t);
plot3(xr,yr,z) ; hold on; plot3(xl,yl,z,'r')
axis equal