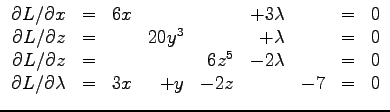- 1a)
- Auf welchen Matrizen-Typ wird die Methode des Vorwärts-Einsetzens
angewandt?
- L1a)
- Auf die aus der L-R-Zerlegung stammende L-Matrix
- 1b)
- Nennen Sie zwei MATLAB Bibliotheksprozeduren,
die beide zur grafischen Darstellung von
Funktionen von zwei Variablen dienen!
- L1b)
contour, contour3, contourf, surf- 1c)
- Bestimmen Sie den Parameter a im Vektor v so dass
die beiden Vektoren u und v zueinander orthogonal sind.
u = [1;2;3]v = [3;2;a] - L1c)
1*3+2*2+3*a = 0, also ista = -7/3- 1d)
- Bestimmen Sie die am einfachsten auszuwertende Formel, um
die Werte der Matrix
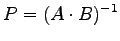 zu erhalten, wenn man weiss, dass sowohl
zu erhalten, wenn man weiss, dass sowohl 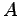 als auch
als auch 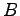 beide orthogonal
sind.
beide orthogonal
sind.
- L1d)
-
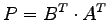
plot(z) vier
vom Nullpunkt ausgehende Strahlen gezeichnet werden.
Die Strahlen sollen gleiche Winkel-Abstände aufweisen und gleiche Länge
haben. Der erste Strahl zeigt von Die komplexen Zahlen in diesem Vektor müssen einzeln angegeben werden, allerdings ist dabei auch die Euler'sche Form erlaubt.
w1 = pi/4; w4 = 3*pi/4; dw = pi/6; r = 2*sqrt(2); z(1) = 0; z(2) = 2*sqrt(2)*exp(i*pi/4) ; z(3) = 0; z(4) = 2*sqrt(2)*exp(i*pi*5/12) ; z(5) = 0; z(6) = 2*sqrt(2)*exp(i*pi*7/12) ; z(7) = 0; z(8) = 2*sqrt(2)*exp(i*3*pi/4) ; plot(z) ; axis equal
Mxz = [1 0 0; 0 -1 0; 0 0 1] an der x-z-Ebene gespiegelt.
Berechnen Sie die Neigung der Ebene ABC gegenüber der Horizontalen (= x-y-Ebene), sowie den Winkel zwischen der Ebene ABC und der zugehörigen gespiegelten Ebene.
Alle Resultate müssen als Zahlenwerte berechnet und angegeben werden, reine Formeln geben in diesem Fall keine Punkte!
% 3G A = [ 0 0 3.2]' ; B = [4 0 0]' ; C = [0 3 0]'; Mxz = [1 0 0; 0 -1 0; 0 0 1]; ABCm = Mxz*[A B C] % Die gespiegelten Vektoren sind fuer A, B identisch, Cm = -C % 2 Vektoren im Innern der Ebene ABC u = B-A; v = C-A; % Kreuzprodukt ergibt Normalenvektor N = cross(u,v); % N= [9.6 12.8 12]; Norm(N) = 20 % Normalenvektor zur Horizontalen ist rein in z-Richtung upvec = [0 0 1]' % Neigung der Ebene ABC w = acosd(upvec'*N/norm(N)) % 53.1301 Grad 0.9273 rad % Winkel zwischen zueinander gespiegelten Ebenen ist das % Doppelte wie der Winkel zur spiegelnden Ebene mirvec = [0 1 0]' wwh = acosd(mirvec'*N/norm(N)) % 50.2082 Grad vv = -C-A; NN = cross(u,vv); ww = acosd(NN'*N/(N'*N)) % 100.4164 Grad 1.7526 rad
A = [-4 -4 0]'; B = [4 -4 0]'; C = [4 4 0]'; D = [-4 4 0]' ; E = [-4 -4 8]'; F = [4 -4 8]'; G = [4 4 8]'; H = [-4 4 8]' ; % 2 Vektoren in Ebene, Kreuzprodukt, Normalenverktor, normieren: u = D - B; v = F - B; N = cross(u,v), en = N/norm(N) % [0.707 0.707 0]' dkrit = en'*B, dchkH = en'*H-dkrit % dkrit = 0, dchkH = 0, OK % Definition der Geraden: A + lam*AM, M=(C+G)/2 M = (C+G)/2 % M= [4 4 4]' r = M-A % r = [8 8 4]' % en'*(A+lam*r) - dkrit = 0 muss erfuellt sein, daraus lamdp lamdp = (dkrit-en'*A)/(en'*r) % = 0.5 Pd = A+lamdp*r % [ 0 0 2]
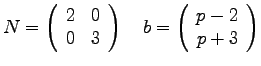
unter den Nebenbedingungen
Es ist nur das Gleichungssystem anzugeben, dieses muss jedoch nicht gelöst werden.