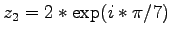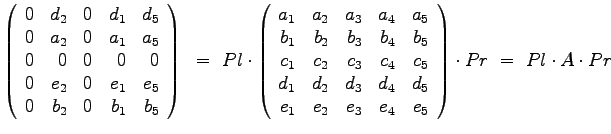


Nächste Seite: FS 10 - Lösungen
Aufwärts: Frühjahrssemester 2010
Vorherige Seite: FS 10 - Prüfung
Inhalt
Y
Ingenieurmathematik Prüfung 1
11.Mai2010
Zeit 90 Minuten, Reihenfolge beliebig, 8 Punkte pro Hauptaufgabe,
40 Pt. = N.6.
- 1)
- Verständnisfragen: Es werden nur ganz kurze
Antworten erwartet.
- 1a)
- Wie nennt man eine Matrix für welche gilt:
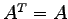
- 1b)
- Geben Sie jeweils die konjugiert komplexe Zahl an zu den beiden Zahlen
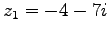 ,
,
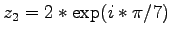
- 1c)
- Wie erreicht man in MATLAB, dass die mit plot gezeichneten
Punkte mit roten Pluszeichen markiert und auch durch eine
rote Linie verbunden werden?
- 1d)
- Geben Sie die MATLAB - Befehle an zum Zeichnen eines
räumlichen Dreiecks als geschlossene Figur, nachdem die Ecken
mit dem Befehlen
P=[2 0 0]' ; Q=[0 5 0]' ; R=[0 0 1]' ;
bereits definiert wurden.
- 2)
- Suchen Sie die speziellen Permutations/Auswahlmatrizen
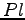 und
und 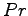 , so dass
die folgende Matrizengleichung für beliebige Werte der Matrix A gilt!
, so dass
die folgende Matrizengleichung für beliebige Werte der Matrix A gilt!
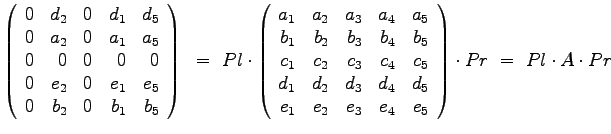
- 3)
- Zwei Schraubenlinien starten beide im Punkt
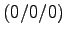 und enden beide im Punkt
und enden beide im Punkt 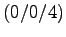 .
Beide haben 2Umgänge und gehen daher auch noch durch den Punkt
.
Beide haben 2Umgänge und gehen daher auch noch durch den Punkt
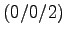 .
.
Die rechtsdrehende Schraubenlinie hat ihre in z-Richtung
verlaufende Achse bei 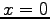 ,
, 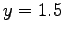 .
Die linksdrehende Schraubenlinie hat ihre
in z-Richtung verlaufende Achse
bei
.
Die linksdrehende Schraubenlinie hat ihre
in z-Richtung verlaufende Achse
bei 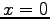 ,
, 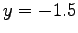 .
.
Bestimmen Sie die Parameter dieser beiden Schraubenlinien und
geben Sie ein MATLAB-Skript an, für die 3D Darstellung dieser beiden
Linen in einem Bild.
- 4)
- Durch die Mittelpunkte der von A ausgehenden Kanten eines Quaders
ABCD EFGH
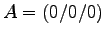
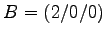
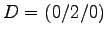
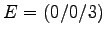 etc.,
(also durch MAB, MAD und MAE)
wird eine Ebene g gelegt.
etc.,
(also durch MAB, MAD und MAE)
wird eine Ebene g gelegt.
Bestimmen Sie diese Ebene in der Hesse'schen Normalform
(d.h. durch Angabe des Normalen-Einheitsvektors en und der
Test-Distanz dkrit).
Bestimmen Sie auch die zu g parallele Ebene, welche durch A geht.
- 5)
- Geben Sie eine MATLAB Funktion an, welche für eine L-Matrix
mit fester Dimension 3x3 und einen Vektor b der Dimension 3x1
den Algorithmus des Vorwärts-Einsetzens löst, der also
y bestimmt aus
L*y = b , ohne
von Schleifenkonstruktionen Gebrauch zu machen.
- 6)
- Geben Sie die 3 komplexen Zahlen an, welche die
Gleichung
![$\displaystyle{z_k = (\,\sqrt[3]{-27}\,)^5}$](img3005.png) erfüllen.
erfüllen.
Bei der Lösung müssen alle Teilschritte angegeben werden,
ein reines Schlussresultat wird nicht bewertet!












Nächste Seite: FS 10 - Lösungen
Aufwärts: Frühjahrssemester 2010
Vorherige Seite: FS 10 - Prüfung
Inhalt
2012-03-21
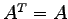
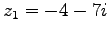 ,
,