FS 08 - Lösungen zur Prüfung 1, B, 8. April 2008

B   Ingenieurmathematik Prüfung 1 8.April2008
Zeit 90 Minuten, Reihenfolge beliebig, 8 Punkte pro Hauptaufgabe, 40 Pt. = N.6.

1)

Verständnisfragen: Es werden nur ganz kurze Antworten erwartet.

1a)

Geben Sie einen Vektor zv (eine Folge) von komplexen Zahlen an, so dass plot(zv); axis equal ein auf der Spitze stehendes Quadrat mit der Seitenlänge 2 zeichnet.

L1a)

zv = sqrt(2)*[ 1 i -1 -i 1] ; plot(zv); axis equal

1b)

Bestimmen Sie die Zahlen n und m , so dass die folgendende Matrixmultiplikation legal ist: A(4x6)*B(6x4)*C(nx5)*D(mx2)

L1b)

n=4; m=5;

1c)

Geben Sie eine 3x3 Turm-Matrix an, für welche gilt 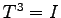$T^3 = I$ (I = Einheitsmatrix)

L1c)

Scroll up oder scroll down; T = [0 1 0; 0 0 1; 1 0 0]; T^3

1d)

Beschreiben Sie wie man die Matrix $G =(E\cdot F)^{-1}$ berechnet, aus der Angabe dass E = [1 0 0; -0.2 1 0; 0 0 1] und F = [1 0 0; 0 1 0; 0 0.5 1] gilt.

L1d)

G = (E*F)^-1 % Fi*Ei =[ 1 0 0; 0.2 1 0; -0.1 -0.5 1]

2)

Suchen Sie die speziellen Permutations/Auswahlmatrizen $Pl$ und $Pr$, so dass die folgende Matrizengleichung für beliebige Werte der Matrix A gilt!

$${ \left( \begin{array}{rrrrr} e_5 & 0 & e_1 & e_4 & 0 \\ 0... ..._2 & e_3 & e_4 & e_5 \end{array} \right) \cdot Pr ~=~ Pl \cdot A \cdot Pr }$$

L2)

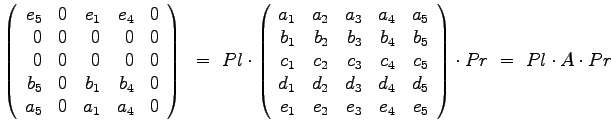
        0     0     0     0     1          0     0     1     0     0
        0     0     0     0     0          0     0     0     0     0
 Pl =   0     0     0     0     0     Pr = 0     0     0     0     0
        0     1     0     0     0          0     0     0     1     0
        1     0     0     0     0          1     0     0     0     0

3)

Suchen sie alle komplexen Lösungen $z_k$ der Gleichung

$$(z-i)^4 + 4 = 0$$

L3)

4 Lösungen für die Klammer: $u_1 = \sqrt{2}*\exp(j*pi/4)$,   $u_2 = \sqrt{2}*\exp(j*3*pi/4)$,   $u_3 = \sqrt{2}*\exp(j*5*pi/4)$ $u_4 = \sqrt{2}*\exp(j*7*pi/4)$
Arithmetische Form $u_1= 1+i$ , also $z_1 = 1+2i$, $u_2= -1+i$ , also $z_2 =-1+ 2i$, $u_3= -1-i$ , also $z_3 = -1$, $u_4= 1-i$ , also $z_4 = 1$,

4)

Gegeben ist der Quader $A(-1/0/0)$ $B(-1/2/0)$ $C(2/2/0)$ $D(2/0/0)$ $E(-1/0/1)$ $F(-1/2/1)$ $G(2/2/1)$ $H(2/0/1)$. Berechnen Sie die Winkel $\alpha$ zwischen den Vektoren AC und AG , sowie $\beta$ zwischen AH und AG

L4)

 A=[-1 0 0]'; B=[-1 2 0]'; C=[2 2 0]'; D=[2 0 0]';
 E=[-1 0 1]'; F=[-1 2 1]'; G=[2 2 1]'; H=[2 0 1]';
u1 = C-A, v1 = G-A, sp1 = u1'*v1, u1b = norm(u1), v1b = norm(v1) 
co1 = sp1/u1b/v1b   % 0.9636
%  u1 = [3 2 0]' ; v1 = [3 2 1]'; sp1 = 13; u1b =  3.6056; v1b = 3.7417
w1 = acos(u1'*v1/norm(u1)/norm(v1))
%    0.2705 rad      15.5014  Grad
u2 = H-A, v2 = G-A, sp2 = u2'*v2, u2b = norm(u2), v2b = norm(v2) 
co2 = sp2/u2b/v2b   %  0.8452
%  u2 = [3 0 1]' ; v2 = [3 2 1]'; sp2 = 10; u2b = 3.1623; v2b = 3.7417
w2 = acos(u2'*v2/norm(u2)/norm(v2))
%    0.5639 rad      32.3115  Grad 
Q = [ A B C D A E F B F G C G H D H E];
plot3(Q(1,:), Q(2,:), Q(3,:),'k'); hold on
UV1 = [G A C]; UV2 = [H A G];
plot3(UV1(1,:), UV1(2,:), UV1(3,:),'r'); axis equal
plot3(UV2(1,:), UV2(2,:), UV2(3,:),'m'); hold off

5)

Bestimmen Sie die Parameterdarstellungen der beiden Schraubenlinien (eine rechts- und eine links-Schraube) die beide im Punkt $0/0/0$ starten, durch die durch die Punkte $(0/2/1)$ $(0/0/2)$ und $(0/2/3)$ gehen und beim Punkt $(0/0/4)$ enden. Geben Sie die MATLAB-Befehle an, um die rechts-Schraube schwarz, die links-Schraube rot und die angegebenen Punkte als grüne Ringe zu zeichnen.

L5)

% Punkte auf vertikalen Linien ueber 0/0 und 0/2
%   Achse bei 0/1,  h = 2  Radius = 1  2 Umgaenge
t = (0:0.01:2)*2*pi; r = 1; h = 2;
yl = 1 - r*cos(t); xl = -r*sin(t) ; zl = t*h/2/pi;
yr = 1 - r*cos(t); xr =  r*sin(t) ; zr = t*h/2/pi;
plot3(xl,yl,zl,'r'); hold on;
plot3(xr,yr,zr,'k'); axis equal;
plot3([0 0 0 0 0], [0 2 0 2 0], [0 1 2 3 4], 'go'); hold off

6)

Geben Sie die Teilmatrizen und die Gesamt-Transformations-Matrix an für die 2D homogene Koordinatentransformation, welche das Rechteck ABCD ($A(1/3)$, $B(11/3)$ ,$C(11/7)$, $D(1/7)$,) um $-90^{\mathrm{o}}$  um seinen Mittelpunkt dreht. Geben Sie auch die Ecken des transformierten Rechtecks an.

L6)

Rur = [1 11 11 1 1; 3 3 7 7 3; 1 1 1 1 1];
%  M = (6/5)  (1+11)/2 , (3+7)/2
Tz = [1 0 -6; 0 1 -5; 0 0 1]; R = [0 1 0; -1 0 0; 0 0 1];
Tb = [1 0  6; 0 1  5; 0 0 1];  TT = Tb*R*Tz %= [0 1 1; -1 0 11; 0 0 1];
Rtr = Tb*R*Tz*Rur % Rtr = [4 4 8 8 4; 10 0 0 10 10; 1 1 1 1 1];
plot(Rur(1,:),Rur(2,:),'k') ; axis equal; hold on
plot(Rtr(1,:),Rtr(2,:),'r') ;
Rzr = Tz*Rur 
plot(Rzr(1,:),Rzr(2,:),'g') ;
Rrr = R*Tz*Rur 
plot(Rrr(1,:),Rrr(2,:),'g') ;