FS 09 - Lösungen zur Prüfung 2, B, 12. Mai 2009

B   Ingenieurmathematik Prüfung 2 12.Mai2009
Zeit 90 Minuten, Reihenfolge beliebig, 8 Punkte pro Hauptaufgabe, 40 Pt. = N.6.

1)

Verständnisfragen: Es werden nur ganz kurze Antworten erwartet.

1a)

Geben Sie eine der beiden Quadratwurzeln von 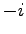$-i$ an.

BL1a)

    zsqr = exp(j*3*pi/4)
    tstsq = zsqr^2
    dum = input('BL1a)  weiter?');

1b)

Mit M = [0 6 3; 0 0 3] sind die Koordinatenpaare der 3 Ecken eines Dreiecks definiert (obere Zeile x, untere y). Mit welchen MATLAB-Befehlen erreichen Sie, dass dieses Dreieck mit allen 3 Seiten unverzerrt gezeichnet wird?

BL1b)

    M = [0 6 3; 0 0 3];
    MM= [M M];  %  Anfangspunkt muss nochmal vorkommen
    plot(MM(1,:),MM(2,:)); axis equal
    dum = input('BL1b)  weiter?');

1c)

Schreiben Sie ein Beispiel auf für eine 3x3 orthogonale Matrix, welche verschieden ist von der Einheitsmatrix.

BL1c)

    Oexa = [0 1 0; 1 0 0; 0 0 1]
    Otst = Oexa'*Oexa
    dum = input('BL1c)  weiter?');

1d)

Warum braucht ein funktionsfähiger Gauss-Algorithmus eine Pivotkontrolle?

BL1d)

    disp('Weil der Algorithmus abbricht, wenn ein 0-Pivot')
    disp('auftaucht, durch das man nicht dividieren kann')
    dum = input('BL1d)  weiter?');

2)

Geben Sie das MATLAB-Skript an zum Zeichnen einer rechtsgängigen Schraubenlinie mit der y-Achse als Schrauben-Achse, dem Anfangs-Punkt $A(0/0/2)$, dem Endpunkt $E(0/4/2)$ und 8 Umgängen.

BL2)

   w = 0:pi/40:8*2*pi;  r = 2
   h = 4/8 , y = w*h/(2*pi);
   z = r*cos(w) ; %  z = r*cos(w) ; 
   x = r*sin(w) ; %  x = r*sin(w) ;
   figure(1); clf
   plot3(x,y,z); axis equal
   dum = input('BL2)  weiter?');

3)

Geben Sie zwei komplexe Zahlenfolgen $oct$ und $hdec$ an, welche beim Zeichnen mit plot(oct) eine geschlossene reguläre Achteck-Figur und mit plot(hdec) ein vollständiges Sechzehn-Eck ergeben. Beide Figuren müssen im Einheitskreis einbeschrieben sein und beide müssen eine Ecke bei 270 Grad d.h. bei $-i$ haben.

BL3)

   figure(1); clf
   wnro = 0:8;  wo = 2*pi*wnro/8  + 3*pi/2; zo = exp(j*wo); 
   wnrh = 0:16; wh = 2*pi*wnrh/16 + 3*pi/2; zh = exp(j*wh);
   plot(zo,'k') ; hold on ;
   plot(zh, 'r');axis equal;  hold off
   dum = input('BL3)  weiter?');

4)

Der Quader ABCD EFGH $A({0}/{0}/0)$ $B({6}/{0}/0)$ $C({6}/{4}/0)$ $D({0}/{4}/0)$
$E({0}/{0}/5)$ $F({6}/{0}/5)$ $G({6}/{4}/5)$ $H({0}/{4}/5)$
wird von zwei zueinander parallelen Ebenen geschnitten: 1. Ebene f durch $Mab,D,H$
2. Ebene g durch $B, Mcd, F$
wobei $Mab$ der Mittelpunkt der Strecke $AB$ ist, und $Mcd$ der Mittelpunkt der Strecke $CD$.
Geben Sie die Hesse'sche Normalformen dieser beiden Ebenen an und berechnen Sie die Durchstosspunkte der Geraden $AG$ durch diese beiden Ebenen.
Die Tatsache, dass die beiden Ebenen f und g zueinander parallel sind, müssen Sie nicht nachprüfen.

BL4)

  figure(1); clf
  A = [ 0 0 0]'; B = [ 6 0 0]'; C = [ 6 4 0]'; D = [ 0 4 0]';
  E = [ 0 0 5]'; F = [ 6 0 5]'; G = [ 6 4 5]'; H = [ 0 4 5]';
  Mab = (A+B)/2; Mcd = (C+D)/2;
  Nf = cross(D-Mab,H-Mab), enf = Nf/norm(Nf)
  dkrf = enf'*Mab, dtD = enf'*D-dkrf, dtH = enf'*H-dkrf 
  eng = enf % Parallele Ebenen
  dkrg = eng'*B,  dtMcd = eng'*Mcd-dkrg, dtF = eng'*F-dkrg
  %  en'*(Vg + lam*rg) - dkrit - 0 
  %  lam = (dkrit - en'*Vg)/(en'*rg)
  laf = dkrf / (enf'*(G-A)) , DPtf = 0 +  laf * G  
  lag = dkrg / (enf'*(G-A)) , DPtg = 0 +  lag * G  
  dum = input('BL4)  weiter?');

5)

Erstellen Sie eine MATLAB Funktion, welche eine quadratische Matrix als Eingabe erhält und daraus (durch Bearbeitung von Einzel-Elementen im Innern einer Doppelschleife) eine symmetrische Matrix erstellt, bei welcher die Werte ab der Diagonalen gegen links unten mit der eingegebenen Matrix identisch sind.

BL5)

  % function Spt = symmcop(M) 
    M = rand(5)
    [nzei,nspa] = size(M); Spt = M;
    for spa = 2:nzei
      for zei = 1:spa-1
        Spt(zei,spa) = Spt(spa,zei); 
      end
    end
    Spt, Tsym = Spt'-Spt
    dum = input('BL5)  weiter?');

6)

Geben Sie die Teilmatrizen und die Gesamt-Transformations-Matrix an für die 2D homogene Koordinatentransformation, welche das gleichseitige Dreieck ABC ($A(0/0)$, $B(10/0)$, $C(\,5\,/\,(5\sqrt{3}/2))$) an der Geraden $y = \sqrt{3}/3 \cdot x$ spiegelt. Geben Sie auch die Ecken des transformierten Dreiecks an.

BL6)

   figure(1); clf
   Dori = [ 0 10 5 0; 0 0 5*sqrt(3) 0;  1 1 1 1]
   w = atand(sqrt(3)/3)
   Rot1 = [ cosd(-w) -sind(-w) 0; sind(-w) cosd(w) 0; 0 0 1]
   Mx = [1 0 0; 0 -1 0 ; 0 0 1]
   Rot2 = [ cosd(w) -sind(w) 0; sind(w) cosd(w) 0; 0 0 1]
   Ttot = Rot2*Mx*Rot1
   Dtr = Ttot*Dori
   plot(Dori(1,:)+0.1, Dori(2,:)+0.1)
   hold on
   axis([-12 12 -12 12]); axis square
   plot([0 0 ],[-12 12],'k')  ;   plot([-12 12 ],[0 0],'k')
   plot([-5 15],[-5*sqrt(3)/3 15*sqrt(3)/3],'k')
   plot(Dtr(1,:), Dtr(2,:),'r')
   hold off
   dum = input('BL6)  weiter?');