- 1a)
- Wie nennt man eine Matrix für welche gilt:
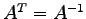
- 1b)
- Geben Sie jeweils die konjugiert komplexe Zahl an zu den beiden Zahlen
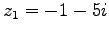 ,
,
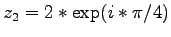
- L1b)
-
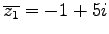 ,
,
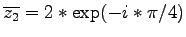
- 1c)
- Wie erreicht man in MATLAB, dass die mit plot gezeichneten
Punkte mit grünen Pluszeichen markiert und auch durch eine
grünen Linie verbunden werden?
- L1c)
plot(x,y,'g+-')- 1d)
- Geben Sie die MATLAB - Befehle an zum Zeichnen eines
räumlichen Dreiecks als geschlossene Figur, nachdem die Ecken
mit dem Befehlen
R=[2 0 0]' ; S=[0 5 0]' ; T=[0 0 1]' ;
bereits definiert wurden. - L1c)
lin = [R S T R]
plot3(lin(1,:) ,lin(2,:), lin(3,:) ); axis equal
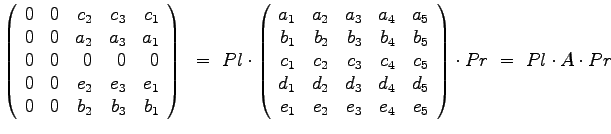
A = [11:15 ; 21:25; 31:35; 41:45 ; 51:55 ] Pl = zeros(5); Pr = zeros(5); Pl(1,3)= 1; Pl(2,1) = 1; Pl(4,5) = 1; Pl(5,2)=1; Pr(2,3)= 1; Pr(3,4) = 1; Pr(1,5) = 1; Rs = Pl * A * Pr
Die rechtsdrehende Schraubenlinie hat ihre in z-Richtung verlaufende Achse bei
Bestimmen Sie die Parameter dieser beiden Schraubenlinien und geben Sie ein MATLAB-Skript an, für die 3D Darstellung dieser beiden Linen in einem Bild.
ntur = 4; h = 2; r = 1; w = (0:0.002:4)* 2 * pi; z = w*h/(2*pi); xl = r*cos(w) -1; yl = -r*sin(w); xr = -r*cos(w) + 1; yr = -r*sin(w); figure(1) clf hold on plot3(xl,yl,z,'g') plot3(xr,yr,z,'r') plot3([0 0 0 0 0], [0 0 0 0 0], [0 2 4 6 8],'ko') axis equal view(-28,40) hold off
Bestimmen Sie diese Ebene in der Hesse'schen Normalform (d.h. durch Angabe des Normalen-Einheitsvektors en und der Test-Distanz dkrit).
Bestimmen Sie auch die zu g parallele Ebene, welche durch A geht.
A=[0 0 0]' ; B = [4 0 0]' ; D = [0 6 0]'; E =[0 0 4]' drb = [A B A D A E] figure(1) clf plot3(drb(1,:), drb(2,:), drb(3,:), 'ko-' ) hold on axis equal MAB = (A+B)/2 MAD = (A+D)/2 MAE = (A+E)/2 eb = [MAB MAD MAE MAB]; plot3(eb(1,:), eb(2,:), eb(3,:), 'r' ) axis equal; hold off v = MAD - MAB w = MAE - MAB N = cross(v,w) % [ 6 4 6 ] eng = N / norm(N) % [0.6396 0.4268 0.6396]' dkritg= eng'*MAB % 1.2782 dtsD = eng'*MAD -dkritg dtsE = eng'*MAE -dkritg enh = eng dkrith = 0 % Ebene durch (0/0/0) hat immer dkrit=0
L*y = b , ohne
von Schleifenkonstruktionen Gebrauch zu machen.
function y = fix3forwsub(L,b) y = zeros(3,1); % y1 kann b1 direkt uebernehmen y(1) = b(1); % div durch 1 , weil L(1,1) = 1 % y1 wird gebraucht weil Element links der Diag nicht 0 y(2) = (b(2) - L(2,1)* y(1) ) % y1 und y2 werden gebraucht weil Elemente links der Diag nicht 0 y(3) = (b(3) - L(3,1)* y(1) - L(3,2)*y(2) )
Bei der Lösung müssen alle Teilschritte angegeben werden, ein reines Schlussresultat wird nicht bewertet!
Z0 = 27 * exp(i*pi) z1 = 27^(1/4) * exp(i*pi/3) z2 = 27^(1/4) * exp(i*(pi/3 +2*pi/3)) z3 = 27^(1/4) * exp(i*(pi/3 +2*2*pi/4)) p1 = 81*exp(i*3*pi/3) p2 = 81 * exp(i*3*(pi/3 +2*pi/3)) p3 = 81 * exp(i*3*(pi/3 +2*2*pi/3))
