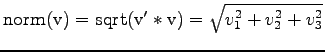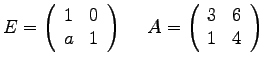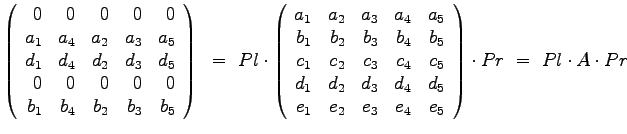


Nächste Seite: HS 10/11 - Prüfung
Aufwärts: Herbstsemester 2010 / 11
Vorherige Seite: HS 10/11 - Lösungen
Inhalt
Grundlagen-Kenntnisse und Arbeitstechniken
Die folgenden Grundlagenkenntnisse und Arbeitstechniken werden in
der Mehrzahl der Aufgaben immer wieder eingesetzt. Es ist daher unerlässlich,
sich diese soweit anzueignen, dass ohne lange Verzögerung darauf
zugegriffen werden kann.
Thema Matrizen
Matrizentypen kennen
Einheitsmatrix, Rechtdreiecksmatrix (= obere Dreiecksmatrix),
Linksdreiecksmatrix (= untere Dreiecksmatrix), symmetrische und antisymmetrische
Matrizen, orthogonale Matrizem
Matrix-Matrix und Matrix-Vektor Multiplikation kennen
und für kleine Dimensionen nachrechnen könnrn.
Multiplikation mit Specht-Matrix
Die Multiplikation mit einer Specht-Matrix (lauter Nullen ausser einer einzigen Eins)
von links bewirkt die Selektion der Zeile mit derselben
Nummer wie die Spalte der Eins
(Selektion bestimmt durch innen aneinanderstossende Indizes)
und das Platzieren in derselben Zeile des Resultates
wie die Zeile der Eins.
Die Multiplikation mit einer Specht-Matrix
von rechts bewirkt die Selektion der Spalte
mit derselben Nummer wie die Zeile der Eins
(Selektion durch innen aneinanderstossende Indizes) und das Platzieren in
derselben Spalte des Resultates
wie die Spalte der Eins.
Matrizen transponieren
Die Dimensionszahlen verden vertauscht und die Elemente über die
Diagonale gespiegelt.
Das Indizieren verstehen
In einer Matrix einzelne Elemente ansprechen
(einspeichern oder herausholen oder ändern)
durch Angabe der beiden Indizes.
Einen Index-Bereich, z.B. eine ganze Zeile oder eine
ganze Spalte oder eine Teilmatrix bezeichnen.
Thema lineare Gleichungssysteme
Den Ablauf der Gauss-Elimination verstehen
Transformation auf R-Form erstellt Nullen in Spalte 1, dann 2, dann 3 bis ndim-1,
immer alle Zeilen ``echt'' unterhalb der Diagonalen.
Für jede Null werden zwei Zeilen kombiniert, zur aktuellen Zeile (mit Faktor 1) wird
die Pivot-Zeile mit dem Faktor f addiert. Damit am gewünschten Ort eine Null entsteht,
muss f = -a(j,k)/a(k,k) gelten.
Die gleiche Kombination b(j) = b(j) + f* b(k)
muss mit den b's der rechten Seiten durchgeführt werden.
Nach Absolvieren der Rechtsdreiecks-Transformation erfolgt die
Berechnung der gesuchten Lösung durch Rückwärts-Einsetzen
im System R*x=btr.
Zusammenhang Gauss L-R-Zerlegung
Die L-R-Zerlegung ist eine Gauss-Elimination, bei welcher ein Protokoll des
Transformations-Ablaufes in der Matix L gespeichert wird.
Für eine beliebige Anzahl von b's der rechten Seiten erfolgt die Lösung
durch die 2 Schritte
1) y bestimmen durch Vorwärts-Einsetzen in L*y = b
2) x berechnen mit Rückwärts-Einsetzen in R*x = y
Mit 1) ist das Mit-Transformieren jederzeit nachholbar.
Lösug mit Q-R-Zerlegung
Die Matrizen, welche von der Bibliotheksprozedur [Q,R] = qr(A)
geliefert werden, ergeben die Lösung zu A*x = b aus
y = Q'*b und Rückwärts-Einsetzen in R*x = y
Thema komplexe Zahlen
Die Multiplikationsformel verstehen
die Formel
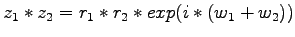 bedeutet,
bedeutet,
dass die komplexe Zahl z1 bei der Multiplikation mit z2 um
den zu z2 gehörenden Winkel w2 gedreht wird und dass der
Betrag r1 um den Betrag r2 gestreckt oder gestaucht wird.
Speziell einfach sind aller reinen Dreh-Zahlen, bei denen der
Betrag 1 ist, also vom Typ zr = exp(i*w), wobei w der Drehwinkel ist
Das komplexe Potenzieren verstehen
Die aufeinanderfolgenden Potenzen einer komplexen Zahl z
entstehen durch weiter-Drehen bei jeder nächsthöheren Potenz,
immer um denselben Winkel w, der zur Zahl z = r*exp(iw) gehört.
Das Prinzip der mehrfachen Wurzeln verstehen
Ausgangspunkt ist die Tatsache, dass jede komplexe Zahl in der
Euler'schen Darstellung unendlich mehrdeutig ist
r*exp(i*w) ist auch r*exp(i*(w+k*2*pi)) für
beliebige ganzzahlige Werte von k.
Das ist ohne weitere Bedeutung für das Rechnen mit komplexen
Zahlen; die verschiedenen Winkel zeigen immer auf dieselbe Zahl.
Ausnahme: Beim Wurzelziehen wird der Winkel durch den
Wurzelnenner dividiert z.B. durch 4. Dadurch entstehen aus
den Winkelwerten von z.B. exp(i*pi), exp(i*3*pi), exp(i*5*pi) und
exp(i*7*pi), welche vor der Division alle auf dieselbe Zahl (-1)
zeigen beim Dividieren die 4 verschiedenen Wurzeln aus -1:
exp(i*pi/4), exp(i*3*pi/4), exp(i*5*pi/4) und
exp(i*7*pi/4)
Erst bei der 5. Version, bei exp(i*9*pi/4) beginnen die Zahlen
wieder mit den schon betrachteten 4 verschiedenen zusammenzufallen
und es ergibt sich nahher nichts mehr Neues.
Thema Vektorgeometrie
Ortsvektor bilden aus gegebenen Koordinaten:
Koordinaten als Komponenten des Ortsvektors einsetzen.
Differenzvektor bilden zwischen zwei Ortsvektoren ergibt
einen normalen Differenzenvektor. v = Vektor von A nach B ist OB - OA.
Norm (Länge) eines Vektors berechnen
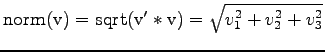
Skalarprodukt zwischen zwei Vektoren (engl. dot-product)
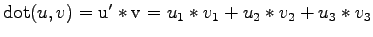
Kreuzprodukt zwischen zwei Vektoren
![$ u \times v = [ u_2* v_3 - u_3* v_2 ,~ u_3* v_1 - u_1* v_3 ,~ u_1* v_2 - u_2* v_1 ]'$](img3587.png)
Mittelpunkt einer Strecke Der Ortsvektor des Mittelpunktes
einer Strecke ist der Mittelwert der beiden Ortsvektoren der Endpunkte.
OM = (OA + OB)/2
Schwerpunkt eines Dreiecks Der Ortsvektor des
Schwerpunktes eines Dreiecks ist der Mittelwert der drei Ecken
OS = (OA + OB + OC)/3
Winkel zwischen zwei Vektoren werden nach der Formel brechnet:
w = acos( u'*v/(norm(u)*norm(v)) )
Falls einer oder beide der beteiligten Vektoren Einheitsvektoren
sind, entfallen die entsprechenden Divisionen durch die Norm.
Thema homogene Koordinatentransformation
Teilmatrizen zum eigentlichen Transformations-Teil
Im eigentlichen Transformations-Teil (obere linke 2x2 Teilmatrix)
gibt es die folgenden Fälle:
1. Keine Transformation, Identität: bei reinen Verschiebungen ist
der obere linke Teil die 2x2 Einheitsmatrix I22 = [1 0 ; 0 1]
2. Achsenspiegelung an y-Achse Myax = [ -1 0 ; 0 1 ]
3. Achsenspiegelung an x-Achse Mxax = [ 1 0 ; 0 -1 ]
4. Punktspiegelung am Koordinatenursprung, identisch mit
Rotation um 180 Grad um den Koordinatenursprung.
MP = [ -1 0 ; 0 -1 ]
5. Rotation um den Koordinatenursprung um den Winkel w
Rw = [ cos(w) -sin(w) ; sin(w) cos(w) ]
Teile der Transformationsmatrix zusammenstellen
Die 2x2 Teilmatrix der eigentlichen Transformation ist links oben,
der Spaltenvektor der Verschiebungen tx,ty ist rechts daneben und
die fixe unterste Zeile ist [0 0 1]
Aufeinenderfolgende Transformationen richtig anordnen
Die zu transformierenden Vektoren oder Nebeneinenderstellungen
von Vektoren müssen immer ganz rechts aussen stehen.
Daher muss jede nachfolgende Transformationsmatrix von links her
heranmultipliziert werden.
Spaltenvektoren zu Koordinatenmatrizen zusammenfügen
Im Prinzip könnte man jeden einzelnen Ortsvektor (in homogenen Koordinaten)
separat durch Multiplikation
mit Transformations-Matrizen abbilden.
Die Formulierung der
homogenen Koordinatentransformation
ergibt aber dasselbe, wenn eine beliebige Anzahl von Spaltenvektoren
nebeneinandergestellt
wird und so eine (3 x npt) Matrix bildet.
Diese Koordinatenmatrizen
kann man (ausser an der Dimension, die nicht quadratisch sein muss)
dadurch von den Transformations-Matrizen unterscheiden, dass in der untersten Zeile
lauter Einsen stehen.
Grundaufgabe Rotation in homogenen Koordinaten
Das Drehen um den Winkel w, um einen Punkt xc/yc ausserhalb
von (0/0) erfolgt in drei Schritten:
1. Verschieben um -xc/-yc, so, dass der gewünschte Drehpunkt in den Nullpunkt (0/0)
verschoben wird.
2. Drehen um den Winkel w um (0/0) mit der Matrix
Rw = [ cos(w) -sin(w) ; sin(w) cos(w) ] in der linken oberen Ecke.
3. Zurück-Verschieben um xc/yc, so, dass (0/0) in den aussen liegenden Drehpunkt
xc/yc verschoben wird.
Grundaufgabe Spiegeln in homogenen Koordinaten
Das Spiegeln an einer beliebigen Geraden erfolgt in 5 Schritten:
1. Verschieben eines geeignet gewählten Punktes auf der Geraden in den Nullpunkt (0/0)
2. Drehen der Geraden (d.h. der Ebene) um einen Winkel um (0/0), so
dass die Gerade mit einer der Achsen
übereinstimmt.
3. Spiegeln an der Achse auf welche man die Gerade soeben abgebildet hat.
4. Zurückdrehen der Geraden (d.h. der Ebene) um 0/0 von der Koordinatenachse in die
ursprüngliche Richtung.
5. Zurück-Verschieben des Punktes (0/0) auf den ursprünglich gewählten Punkt.
Falls die Gerade durch den Nullpunkt geht, entfallen 1 und 5.
Falls sie parallel zu einer Koordinaten-Achse liegt entfallen 2 und 4.
Einzel-Kommentare zu den Aufgaben
- 1)
- Verständnisfragen: Es werden nur ganz kurze
Antworten erwartet.
- 1a)
- Beim Matrizenprodukt P=A*B*C*D sind die Dimensionen
von A (4x4), von B(wx5),
von C (5xu) und von D(3x6).
Bestimmen Sie w und u, so dass das Produkt legal ist, und
geben Sie die Dimensionen von P an.
- Bem1a)
- Die Regeln der Matrix-Multiplikation anwenden (innen aneinanderstossende
Dimensionszahlen müssen übereinstimmen und die
äusseren Dimensionen ergeben die
Dinmensionszahlen des Produktes). Aufgabe lesen!
und 2. Teilfrage nicht vergessen.
- 1b)
- Geben Sie zwei komplexe Zahlen z1 und z2 an, so dass eine beliebige Zahl z
durch Multiplizieren mit z1 um 120 Grad und mit z2 um 270 Grad in
der Gauss'schen Zahlenebene gedreht wird (bei gleichbleibendem Betrag).
z1, z2 können in beliebiger Form angegeben werden.
- Bem1b)
- Reines Drehen erfolgt mit komplexen Zahlen des Typs 1*exp(i*w) , wobei der
Winkel w in radian angegeben werden muss. Also z1 = exp(i*2*pi/3)
und z2 = exp(i*3*pi/2)
- 1c)
- Bestimmen Sie den Wert
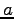 in der
untenstehenden Eliminationsmatrix
in der
untenstehenden Eliminationsmatrix 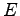 , so dass
, so dass 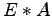 eine Rechtsdreiecks-Matrix ist. Geben Sie auch diese Matrix
eine Rechtsdreiecks-Matrix ist. Geben Sie auch diese Matrix 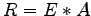 an!
an!
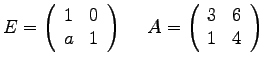
- Bem1c)
- Jeder Gauss-Schritt entspricht einer Multiplikation von links mit
einer derartigen Eliminationsmatrix. Die zu bearbeitende Zeile wird mit
dem Faktor 1 übernommen und dazu die Pivotzeile mit
dem Kombinationsfaktor a (oder auch f genannt) dazugezählt.
Der Faktor a wird so gewaehlt, dass am gewünschten Ort eine Null entsteht.
Hier ist also a = -1/3 und somit R = [3 6 ; 0 2].
- 1d)
- Geben Sie zum Vektor
v = [3 ; 1]
die beiden Produkte (Skalarprodukt) s = v'*v und
(dyadisches Produkt)
Mv = v*v' an!
- Bem1d)
- Skalarprodukt: u1*v1 + u2*v2 = 3*3 + 1*1 = 10
dyadisches Produkt Mv = [3*3 3*1 ; 1*3 1*1] = [ 9 3 ; 3 1]
- 2)
- Suchen Sie die speziellen Permutations/Auswahlmatrizen
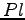 und
und 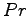 , so dass
die folgende Matrizengleichung für beliebige Werte der Matrix A gilt!
, so dass
die folgende Matrizengleichung für beliebige Werte der Matrix A gilt!
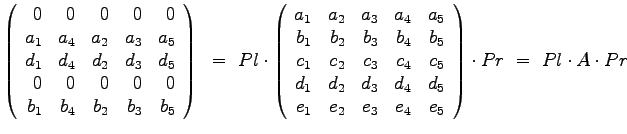
- Bem2)
- Aufspalten in Spechtmatrizen!
extbfPl: 1. Zeile lauter Nullen;
2. Zeile platziert die erste des Originals, also Pl(2,1) = 1;
in 3. Zeile wird die 4. des Originals geholt: Pl(3,4)=1;
4. Zeile Nullen ;
5. Zeile holt 2. des Originals, also P5,2) = 1.
Pr: für 1. Sp die 1. des Originals P1(1,1) = 1;
für 2. Sp die 4. des Originals, also P(4,2) = 1;
für 3. Sp die 2. des Originals, also P(2,3) = 1;
für 4. Sp die 3. des Originals, also P(3,4) = 1;
für 5. Sp die 5. des Originals, also P(5,5) = 1;
- 3)
- Eine rechtsgängige Schraubenlinie mit der Achse auf der
z-Achse startet im Punkt
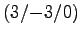 und endet im Punkt
und endet im Punkt 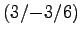 .
Sie hat 3 Umgänge und geht daher auch noch durch die Punkte
.
Sie hat 3 Umgänge und geht daher auch noch durch die Punkte
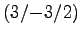 und
und 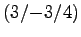 .
Bestimmen Sie die Parameter-Darstellung der Schraubenlinie.
Achten Sie auf den richtigen
Startwinkel, damit die Kurve
durch die vorgegebenen Punkte geht! Bestimmen Sie auch die 3 Punkte,
der Schraubenlinie, welche in
der yz-Halb-Ebene mit positivem y liegen.
.
Bestimmen Sie die Parameter-Darstellung der Schraubenlinie.
Achten Sie auf den richtigen
Startwinkel, damit die Kurve
durch die vorgegebenen Punkte geht! Bestimmen Sie auch die 3 Punkte,
der Schraubenlinie, welche in
der yz-Halb-Ebene mit positivem y liegen.
- Bem3)
- Im Grundriss erscheint die Schraubenlinie als Kreis.
Mit dem Einzeichnen der Punkte und der Achsenposition im Grundriss
werden der Radius und der Anfangswinkel bestimmt.
Für Punkte auf anderen Winkelpositionen muss der
Anstieg aus der Winkeldifferenz zwischen Anfangspunkt
und zu bestimmendem Punkt sowie der Ganghöhe bestimmt werden.
- 4)
- In Oktaeder NESW-TB (Nord, East, Sued, West, Top, Bottom)
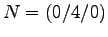 ,
, 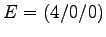 ,
, 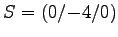 ,
, 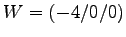 ,
,
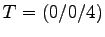 ,
, 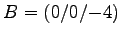
werden zuerst die Mittelpunkte MST und MNT der Kanten ST und NT bestimmt.
Dann soll die Hesse'sche Normalform der Ebene durch die
Punkte E, MST, MNT
bestimmt werden.
Berechnen Sie damit den Abstand der Punkte T, W und 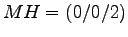 von der
soeben bestimmten Ebene.
von der
soeben bestimmten Ebene.
- Bem4)
- 1. Mittelpunkte der Strecken ST und NT bestimmen,
2. Vektoren in
Ebene z.B u = MST - E, v = MNT - E;
3. Kreuzprodukt N = uxv;
4. Norm von N bestimmen;
5. en = N/norm(N);
6. dkrit bestimmen, mit Ortsvektor von Punkt in Ebene, z.B. aus en'*E;
7. Nacheinander Punkte T, W, MH am Platz von OP einsetzen in Formel en'*OP - dkrit.
- 5)
- Das Quadrat ABCD
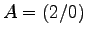 ,
, 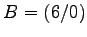 ,
, 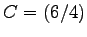 ,
, 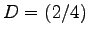 soll mit homogener Koordinatentransformation
um den Punkt A um 180 Grad gedreht werden.
soll mit homogener Koordinatentransformation
um den Punkt A um 180 Grad gedreht werden.
Anschiessend ist das gedrehte Quadrat noch an der x-Achse zu spiegeln.
Geben Sie alle Teil-Transformations-Matrizen fuer diese Abbildungen
in homogenen Koordinaten der Ebene an, sowie die Endkoordinaten
der Eckpunkte und die
Gesamt-Transformationsmatrix dieser Abbildungs-Abfolge.
Es werden in
konkreten Zahlenwerten angegebene Matrizen und Vektoren (bzw.
Koordinatenpaare) verlangt.
- Bem5)
- 1. Spaltenvektoren zu A, B, C, D, (ev. nochmals A) nebeneinanderstellen;
2. Drehung um Äusseren Punkt A mit 3 Transformationsmatrizen formulieren
3. Spiegelung an x-Achse dazufügen;
4. Gesamt-Matrix in richtiger Reihenfolge zusammenmultiplizieren;
5. Koordinatenmatrix von links mit Gesamt-Transformation multiplizieren
- 6)
- Im Würfel
ABCD EFGH
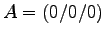
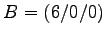
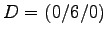
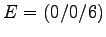 etc.,
soll der der Mittelpunkt MCG der Kante CG berechnet werden und dann
die beiden Winkel
etc.,
soll der der Mittelpunkt MCG der Kante CG berechnet werden und dann
die beiden Winkel
a) zwischen den Vektoren B-MCG und B-G und
b) zwischen den Vektoren B-MCG und B-H
- Bem6)
- 1) Mittelpunkt von CG bestimmen;
2) Vektoren u = MCG - B und v = G - B;
3) Winkel zwischen u und v nach Formel berechnen;
4) Vektoren u = MCG - B und v = H - B;
5) Winkel zwischen u und v nach Formel berechnen;












Nächste Seite: HS 10/11 - Prüfung
Aufwärts: Herbstsemester 2010 / 11
Vorherige Seite: HS 10/11 - Lösungen
Inhalt
2012-03-21