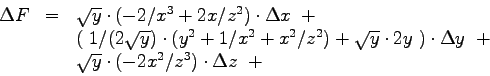- 1a)
- Geben Sie zwei arithmetische Operationen an, welche aus einer komplexen
Zahl und der zugehörigen konjugiert komplexen Zahl ein reelles
Resultat erzeugen!
- L 1a)
-
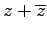 und
und
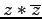
- 1b)
- Wieviele Nullen hat es in einer nxn Permutationsmatrix?
- L 1b)
- n*n-n
- 1c)
- Wie nennt man die speziellen Lösungsverfahren, welche
ein Gleichungssystem effizient lösen, falls die
zugehörige
Matrix eine Rechts- oder eine Linksdreiecksmatrix ist.
- L 1c)
- Rückwärtseinsetzen, Vorwärtseinsetzen
- 1d)
- Wie lautet der MATLAB-Befehl, um die zu zeichnenden
Punkte mit den Koordinatenvektoren xpl und ypl in einem Plot-Aufruf
durch blaue Kreise zu markieren?
- L 1d)
- plot(xpl,ypl,'bo')
w=180/pi*acos(n'*[0 0 1]'/norm(n)) = 48.52
n=8; M=zeros(n);
for zei = 1:n
for spa = 1:zei
if (zei^2 + spa^2)<1.5*n^2
M(zei,spa) = 5;
end
end
end
en'*OP -1.7457 = 0 ; dA = -1.7457 ; dC,F,H = 1.7457 ; dG = 3.491
T1 = [1 0 0; 0 1 -6; 0 0 1]; Mx = [1 0 0; 0 -1 0; 0 0 1]; T2 = [1 0 0; 0 1 6; 0 0 1]; L = [4 4 5; 2 0 0; 1 1 1] T3 = [1 0 -4; 0 1 -12; 0 0 1]; R = [0 -1 0; 1 0 0; 0 0 1]; T4 = [1 0 4; 0 1 12; 0 0 1] Ttot = T4*R*T3 * T2*Mx*T1 % = [ 0 1 4; 1 0 8 ; 0 0 1]; % Ltr = [6 4 4; 12 12 13; 1 1 1]